Voucher System verification using TLA+
By Santhosh Raju, Kamil Rytarowski
- 12 minutes read - 2480 words
Continuing from our previous article, let us take an example of how to write a TLA+ proof for a real-world specification of a distributed system. For this exercise we will go through the Voucher Trading System process as specified by the RFC3506 hosted by IETF. The distributed and concurrent systems require a consensus protocol to achieve overall system reliability and immunity to failures of nodes. We decided to select for this VTS network a simple Two-phase commit protocol.
This article presents how TLA+ and formal methods in general assure correctness of the defined specification, in our case, of the VTS network and the distributed consensus implementation. Preparing a formal proof guarantees the 1-to-1 match between a specification and the implementation. This property of formal methodology verifies not just the fultlessness of a specification, but catches possible flaws or wrong assumptions in a system at a very early stage and allows fixing them before it could be too late or too costly.
If you want to avoid your product to implode, and easily catch a set of flaws in the specification itself and in an implementation itself, learn more about TLA+.
An introduction to consensus protocol
Consensus protocol is a mechanism in distributed computing networks where the participating nodes propose values and all of them have to agree on one of the proposed values.
This mechanism assures that all interacting entities can do a transaction without entering into conflicting conditions and always leading into well defined accomplished transaction states. The aim is to make the overall system fault-tolerant and resillent, protecting the network from security attacks and guaranteeing scalable and efficient implementation of its application.
The elementary properties of consensus protocol are:
- Validity - any value decided is value proposed.
- Consistency - no two correct nodes decide differently.
- Termination - every correct node eventually decides.
- Integrity - a node decides at most once.
Consensus protocol plays the key role in distributed IoT networks, load balancing, clock synchronization, robotics, blockchain systems and many more.
Two-phase commit (abbreviated as 2PC) is a specialized version of the consensus protocol and consists of two phases:
- Phase 1 The request to prepare phase, in which a coordinator process attempts to prepare all the transaction’s participating processes.
- Phase 2 The commit or abort phase, in which the coordinator decides whether to commit or abort the transaction and notifies the result to all the participant processes.
2PC is a simple mechanism of atomic commitment protocol and it is used in the VTS network, where the coordinator (or arbiter) is the centralized or distributed Voucher Trading Provider and participating nodes consist of: issuers, holders and collectors. The participating nodes exchange vouchers upon which the consensus is made.
Prelude
Before we go deeper into TLA+, we need a general introduction to RFC3506.

RFC3506 is a specification titled as “Requirements and Design for Voucher Trading System (VTS)”. It describes how to do trading of vouchers (think of discount coupons). We will be looking at the process of issuing a voucher as described in the description in RFC in the chapters “Background”, “Terminology” and “Model and VTS Requirements”.
Let’s define the necessary terminology regarding the voucher system:
- Issuer - An entity who can issue vouchers with a promise.
- Holder - An entity who can hold vouchers that are issued.
- Collector - An entity who can collect the voucher and deliver the promise in the voucher.
- Voucher - A digital representation of an “agreement” that is traded among various entities.
- Voucher Trading Provider (VTP) - An agreed upon arbiter which helps carry out the various operations between the entities and the voucher.
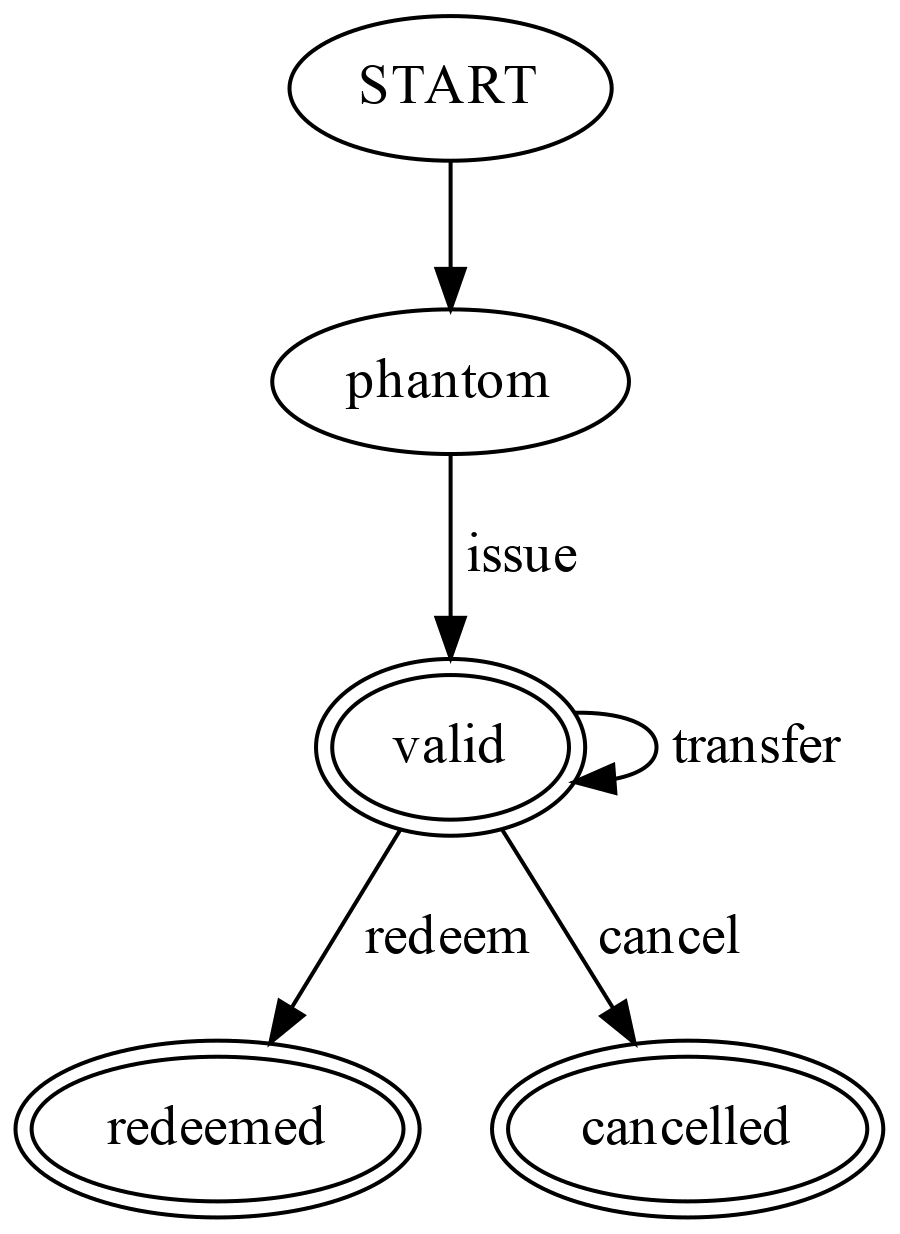
In addition to the above, we also define a Finite-state Machine for the voucher life cycle: this is a simple state machine that makes sure the voucher is in the correct state at any given point in time. Think of this as similar to the state of the turnstile from the example that was mentioned in the previous article.
-
Phantom - This is a new meta state introduced (not present in RFC3506), to indicate a voucher which has not yet been issued. This state is held by vouchers taking part in an issue transaction, when the transaction aborts, these vouchers will cease to exist.
-
Valid - This is the state of voucher that is valid for transfer or redeeming.
-
Redeemed - This indicates the “agreement” or “promise” in the voucher which has been delivered and is no longer valid.
Finally, we also bring in the already described Two-phase commit protocol which helps with the consensus part of the “trading” of vouchers. We use the TLA+ proof given by Leslie Lamport as our starting point to write up the proofs for the “trading” of vouchers.
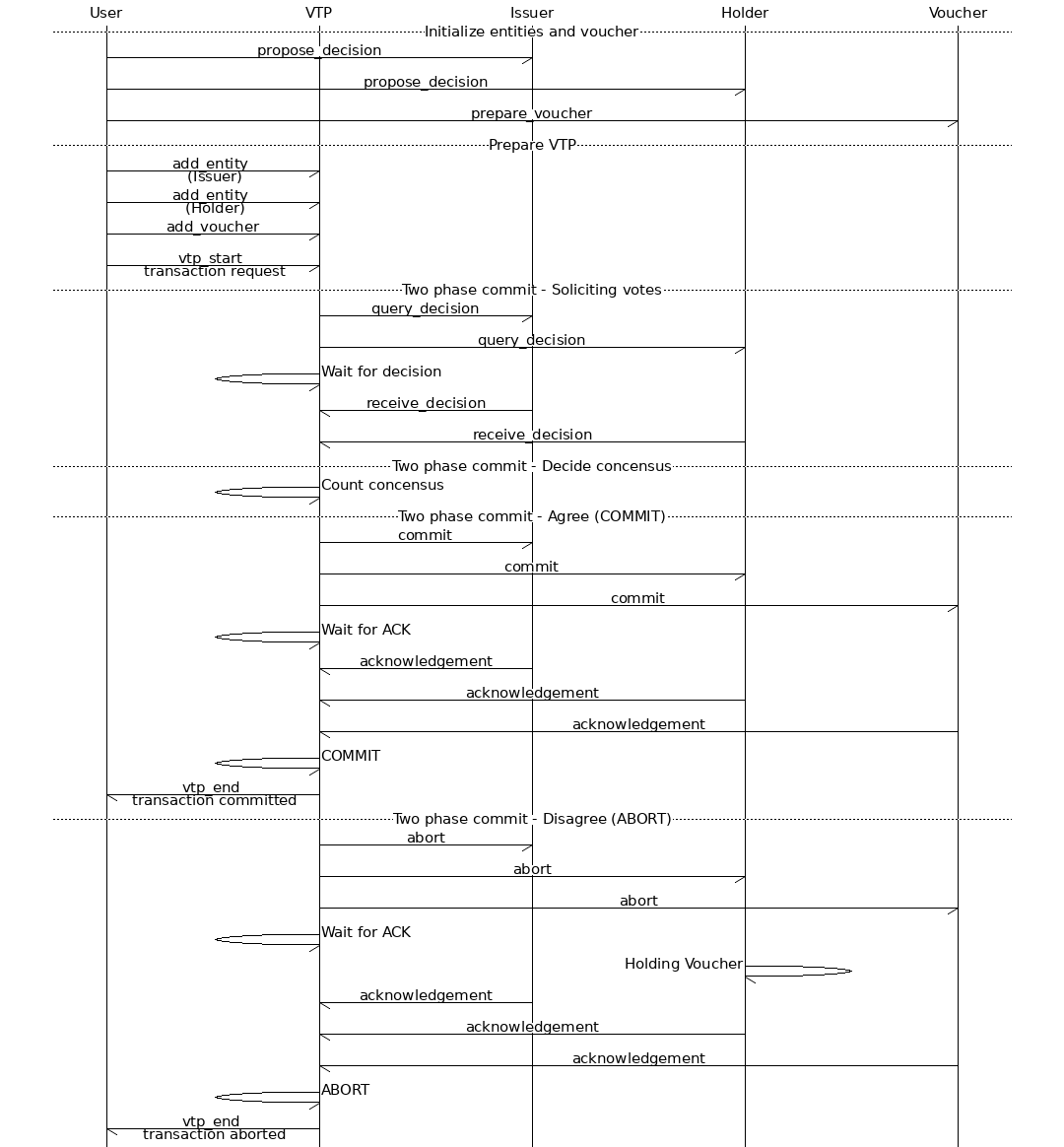
To present a model of our voucher network and write a TLA+ proof for it, we start with a simplified case of exactly one Issuer and one Holder trying to “issue” or “abort” a voucher transaction. To illustrate the workflow of six possible operations with the Two-phase commit protocol network, we present a message sequence diagram and include in it the User, Issuer, Holder, Voucher and VTP. The User and Voucher from a technical point of view are not participating nodes in the network, but for the sake of simplicity we include them in the drawing.
The operations are as follows:
- Propose a decision for each of the Issuer and Holder of the Voucher.
- Prepare the Voucher for the transaction.
- The Issuer, Holder and the Voucher are added to the VTP.
- The VTP queries for the decision of the issuer and holder.
- If all the parties are in agreement VTP commits the transaction and the voucher is issued.
- If no parties can come to an agreement, VTP aborts the transaction and the voucher is not issued.
We are now ready to break this down into a formal proof in TLA+.
Writing the TLA+ proof
Writing TLA+ proofs would be similar to writing up code for a program but with some additional attributes. We have the usual programming language features like constants, variables and functions; however, they look more mathematical to what we might expect from a typical programming language like C/C++, Python, Go or Rust. In order to write the formal proof, we need to use some further specifics of the TLA+ syntax, going beyond the already presented knowledge from the previous article, where we solved the Die Hard problem with two jugs.
-
Messages - One of the things that have to be taken into account when designing a concurrent and distributed system is that the participants within the system will need to communicate with one another. This results in implementation of multiple ways of passing messages across processes (for example pipes, sockets etc). Even though TLA+ does not go into specifics of how this communication is implemented, all we need to know is that TLA+ abstracts all the various types of communication among entities as passing around “messages” among them.
Messages == [type : {"Prepared"}, vi : I] \cup [type : {"Prepared"}, vh : H] \cup [type : {"Issue", "Abort"}] -
Initial State - Any system within our specification should have a well defined initial state, this is equivalent to initializing the start of the program setting up the variables, entry point etc. Our simulation always begins in this state regardless. For a simple Finite-state Machine this would be the “Start” state.
VTPInit == (*****************************************************) (* The initial predicate. *) (*****************************************************) /\ vState = [v \in V |-> "phantom"] /\ vlcState = [v \in V |-> "init"] /\ hState = [h \in H |-> "waiting"] /\ iState = [i \in I |-> "waiting"] /\ vtpState = "init" /\ vtpIPrepared = {} /\ msgs = {} -
Next state - This is usually a combination of various possible states that is allowed from the initial state and also includes the final states that would be reached by the system we are trying to verify. Each of the states is represented by something that looks like a function call representing an operation that is allowed for the state.
VTPNext == \/ \E v \in V: VTPIssue(v) \/ VTPAbort(v) \/ \E h,i \in H \cup I: VTPRcvPrepared(h,i) \/ \E h \in H: HPrepare(h) \/ HChooseToAbort(h) \/ HRcvAbortMsg(h) \/ HRcvIssueMsg(h) \/ \E i \in I: IPrepare(i) \/ IChooseToAbort(i) \/ IRcvAbortMsg(i) \/ IRcvIssueMsg(i)In the above example, the definition of
VTPIssue(v)describes the state of the system once a voucher has been issued, where we have to make sure the following things are correct.- The initial state of the voucher is “phantom”, i.e. the voucher does not exist yet.
- The voucher life cycle machine is currently in “init” state.
- The voucher transaction provider is currently in the “init” state.
- The Holder and Issuer are in the Prepared state.
Once the above states are true, we “issue” the voucher and the next expected states are
- The voucher transaction provider is in “done” state.
- The voucher’s state has become “valid”, only the voucher which the entities were exchanging has actually switched to this state.
- The voucher life cycle machine has switched over to “working” state.
- Make sure the “message” for the operation “Issue” has arrived in the messages list.
In addition to the above, we also make sure things that were not supposed to “change” have not changed, this is quite important to make sure that our state transition has not caused any unwanted side effects.
In this way we define the various states that the system can be in using our TLA+ specification.
-
Invariants - This is a very important part of writing TLA+ specifications, an invariant can easily be described by asking “what are the things within the system that cannot change”. In other words, if the invariants of a system change with time, then the definition of the system or the assumptions made about the system do not hold up.
There are two kinds of invariants in our example
-
Type Invariant - This is basically what the allowed states are for the various state machines in our system. An example of a type invariant violation would be to have a state called “redeemed” in our Voucher Issue operation. Another example is if the state of the voucher in the system goes to “invalid” in the issue process.
VTPTypeOK == (*****************************************************) (* The type-correctness invariant *) (*****************************************************) /\ vState \in [V -> {"phantom", "valid"}] /\ vlcState \in [V -> {"init", "working"}] /\ hState \in [H -> {"waiting", "prepared", "holding", "aborted"}] /\ iState \in [I -> {"waiting", "prepared", "issued", "aborted"}] /\ vtpState \in {"init", "done"} /\ vtpIPrepared \subseteq (H \cup I) /\ msgs \subseteq Messages -
Consistency Invariant - This is another invariant that makes sure that we do not end up with conflicting states for our “Holder” and “Issuer”, for example it would not make sense if the “Holder” aborted the transaction but the “Issuer” issued the voucher.
VTPConsistent == (*****************************************************************) (*A state predicate asserting that a H and an I have not reached *) (*conflicting decisions. It is an invariant of the specification.*) (*****************************************************************) /\ \A h \in H, i \in I : /\ ~ /\ hState[h] = "holding" /\ iState[i] = "aborted" /\ ~ /\ hState[h] = "aborted" /\ iState[i] = "issued"
-
Finally, the proof is complete when we put all this together and define this as our specification as shown in line 255 of our Voucher Issue TLA and then add the invariant to this proof.
THEOREM VTPSpec => [](VTPTypeOK /\ VTPConsistent)
We repeat this process for the various transactions that are defined in RFC3506.
Conclusion
Writing a formal verification system is a process that takes a high amount of discipline and rigor. The hardest part of this would be breaking down the system into various independently verifiable components and identifying the correct invariants for these breakdowns. For instance, in this above example we have not considered the verification of the state machines of the Issuer, Holder or Voucher. Designing a system requires you to write proofs for these too for the sake of completeness.
TLA+ catches easily flaws that involve getting into state transitions that may not be allowed.
As an illustration in our voucher life-cycle we should never have Phantom Voucher ever go into a redeemed state.
And when we combine the proof of the Voucher Life Cycle
with that of the Voucher Redeem, we can verify that the simulation of Voucher
Redeem would not violate the state machine described by the Voucher Life Cycle.
This can be seen as INSTANCE VoucherLifeCycle in
VoucherRedeem.tla#L273.
Unfortunately, not every single flaw can be detected by TLA+. An example of such a mistake is an incorrect assumption in the invariant type. One can define the various states in a system and if we missed out or wrongly defined a type invariant of the system, TLA+ would not catch it.
For example, a message which was supposed to be passed between the entities could be overlooked:
Messages ==
[type : {"Prepared"}, vi : I] \cup
[type : {"Prepared"}, vh : H] \cup
[type : {"Issue", "Abort"}]
We have missed out the “Prepared” messages for the individual entities, which were defined as:
Messages ==
[type : {"Issue", "Abort", "Prepared"}]
The TLA+ simulation will see the “Prepared” message, but would not know if the prepared was from Issuer or Holder. More importantly, the formal verification tool might only “see” one of the messages. An example of this would be the Issuer sending the “Prepared” message but not the Holder, and since our Messages does not specifically say if the “Prepared” came from a specific entity, our Type invariant would not be violated but our TLA+ specification might be wrong. The “Prepared” message example was taken from the real-life from our former project and it was fortunately caught quickly. Unfortunately (but not unsurprisingly), no single tool can prevent mistakes performed by developers and there is a need for a prior experience.
For large systems and the process of formal software verification, the system should behave as we observe in the simulation so it can be used to verify if the behavior expected is the same as the behavior observed.
Hopefully this brief introduction gives you an idea on what to expect from writing up formal specifications in TLA+ and a general guideline to set proper expectations when working with TLA+.
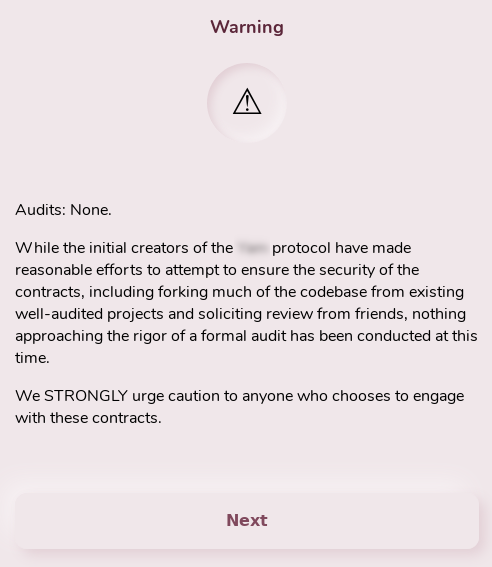
Unfortunately, as presented on the screenshot above from one of the recent cryptocurrency failures, not every vendor audits its products and this can affect not only the business but also impact the investments from the venture capital and regular people who put their money into a new product. In the world changing towards more proven and trusted technologies, the formal verification is getting a more and more important role.
Do not hesitate to formally check your products before the cost of detecting and addressing a flaw can be negligible compared to the cost of pushing your product out of the market and depleting your business model.